
Bauregeln gotischer Kathedralen, auch am Überlinger Münster?
Carl Fahr, 2024
„ad quadratum“ und „ad triangulum“ eine Untersuchung dieser Bauregeln am Überlinger Münster

Bei Osiander fand ich das Buch von
Malcolm Hislop: „Wie baut man eine Kathedrale“.
Interessant geschrieben und bebildert mit vorwiegend französischen und englischen Kathedralen. Ich stieß unter anderem auf ein Kapitel über geometrische Regeln, die von den Baumeistern der großen gotischen Kathedralen angewendet wurden.
Hier las ich:
Die Geometrie ist das Herz der Entwürfe mittelalterlicher Kathedralen, denn die Proportionen von Entwürfen, Profilen und Fassaden wurden aus geometrischen Figuren abgeleitet. Sogar Details wie Kreuzblumen, Fenstermauerwerk und Zierleisten basieren auf geometrischen Figuren und wurden mit Zirkel und Winkelmaß gezeichnet.
Der Gesamtentwurf einer Kirche beruhte also auf der Geometrie mit ihren Regeln der Proportionalität. Am bekanntesten war die Gleichung 1: √2 (1:1,41), die das Verhältnis der Seite eines Quadrats zu seiner Diagonalen darstellt und daher leicht zu behalten und zu konstruieren war.
Wenn es diese Regeln gab, wurden sie dann auch von den Baumeistern des Überlinger Münsters angewandt?
Dies war die spannende Frage, der ich anhand meiner dreidimensionalen CAD-Zeichnungen auf der Basis vorhandener Aufmaßpläne von 1908 /1924 nachgehen wollte.
Und davon möchte ich hier berichten.
Was besagten also diese Regeln, die man „ad quadratum“ und „ad triangulum“ nannte, wie konnte man dies darstellen und wurden sie wirklich auch beim Bau des Überlinger St. Nikolaus Münsters angewandt?
Die Regel „ad quadratum“ besagt: das Verhältnis der Seite eines Quadrats zu seiner Diagonale wird als besonders harmonisch empfunden.
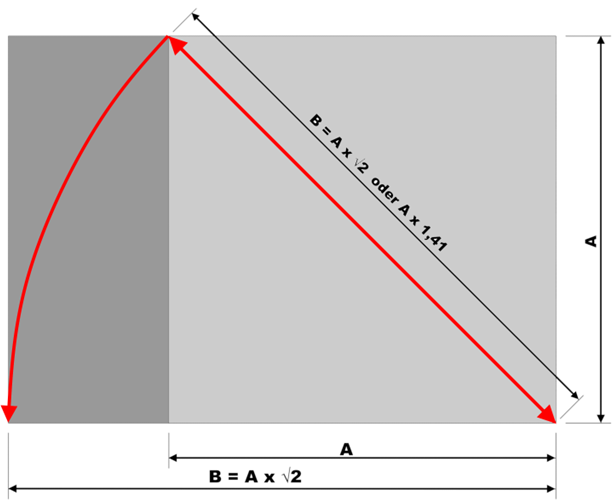
hier ist dargestellt:
auf der rechten Seite ein hellgraues Quadrat, in das rot eine Diagonale eingezeichnet ist. Diese ergibt die Längsseite eines leicht zu konstruierenden und als harmonisch empfundenen Rechtecks
A. „ad quadratum“ untersucht am Grundriss
Dies ist der Grundriss eines Jochs / eines Gewölbefeldes im Mittelschiff des Überlinger Münsters
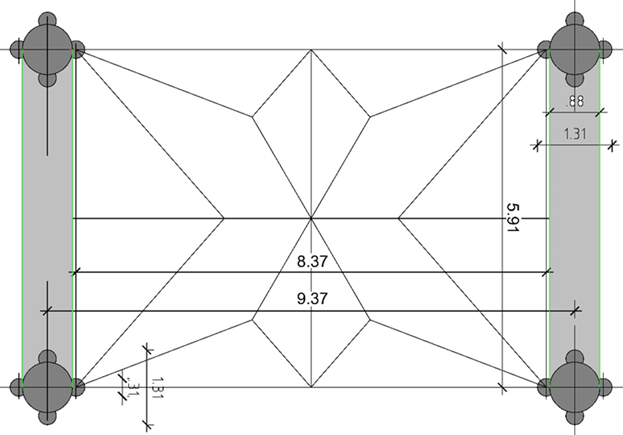
Das Joch ist in der Stützenachse gemessen 9,37m breit und 5,91m lang. Das Mauerwerk oberhalb dieser Mittelschiffsäulen ist 88 cm stark.
Die Mittelschiffsäulen werden begleitet von Halbsäulen (Diensten) mit einem Durchmesser von 31 cm. (Ansicht links)
Im Mittelpunkte dieser Dienste liegen die Zentren der Gewölbeauflager, ihr Abstand: quer = 8,37m, längs = 5,91m.
Zur Bauzeit wurde in Elle oder Fuß gemessen, eine Elle = 59,1cm. (lt. Wikipedia in Stein am Rhein). Das Grundmaß eines Jochs mit 10 x 14 Ellen würde danach 5,91m x 8,274m betragen. Die Differenz zu den Aufmaß-Werten beträgt in der Breite 9,6 cm.
Die folgende Zeichnung zeigt ein Rechteck nach den Regeln des „ad quadratum“ auf der Basis eines Quadrats mit einer Kantenlänge von 10 Ellen. Seine Größe 8,358m quer und 5,91m längs zur Schiffsrichtung
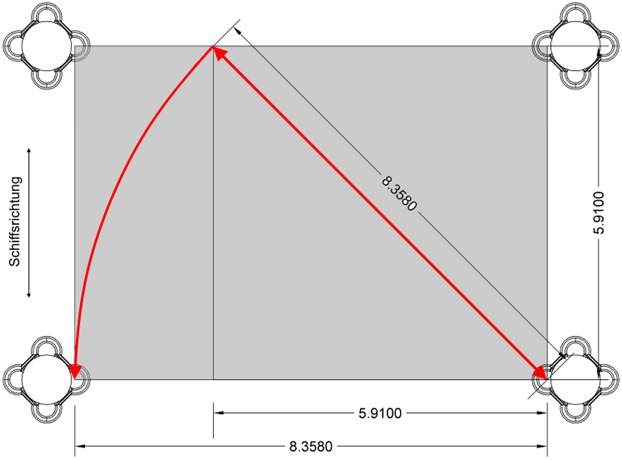
Der Achsabstand der Mittelpunkte der Dienste beträgt also quer zum Mittelschiff:
- lt. Aufmaß = 8,370m,
- 14 Ellen à 0,591m wären = 8,274m,
- geometrisch ermittelt = 8,358m
Die Differenz zum Aufmaß, das während der Sanierung 1908-1924 gemacht wurde, beträgt also
- zum Maß in Ellen = 9,6cm
- zum geometrisch ermittelten Maß = 1,2cm
Das Ergebnis dieser Überlegungen:
Im Grundriß des Überlinger Münsters finden wir die Anwendung der Regel des „ad quadratum“ bestätigt.
B. „ad quadratum“ untersucht am Aufriss
Wurde die Regel des „ad quadratum“ auch im Aufriss, in der Höhenentwicklung angewendet?
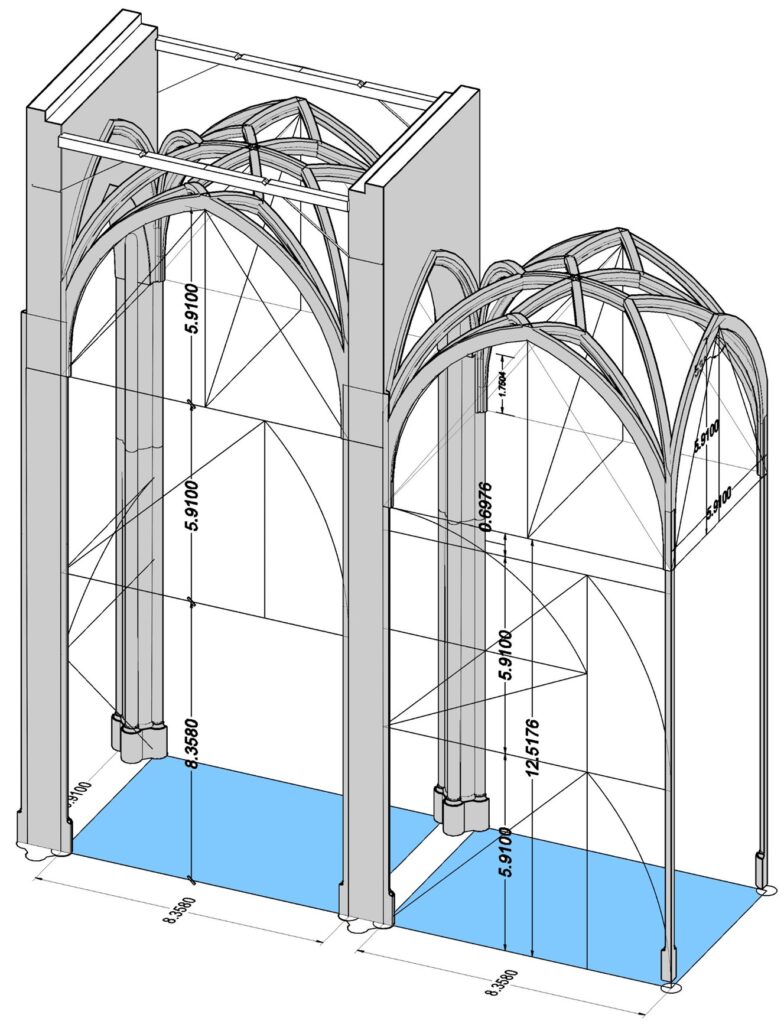
Dieses 3-dimensionale Modellbild zeigt die ursprüngliche Planung von 1420: links das Mittelschiff und rechts das etwas niedrigere Seitenschiff.
Beide Schiffe haben die gleiche Grundfläche von 5,91m x 8,358m (hier blau dargestellt).
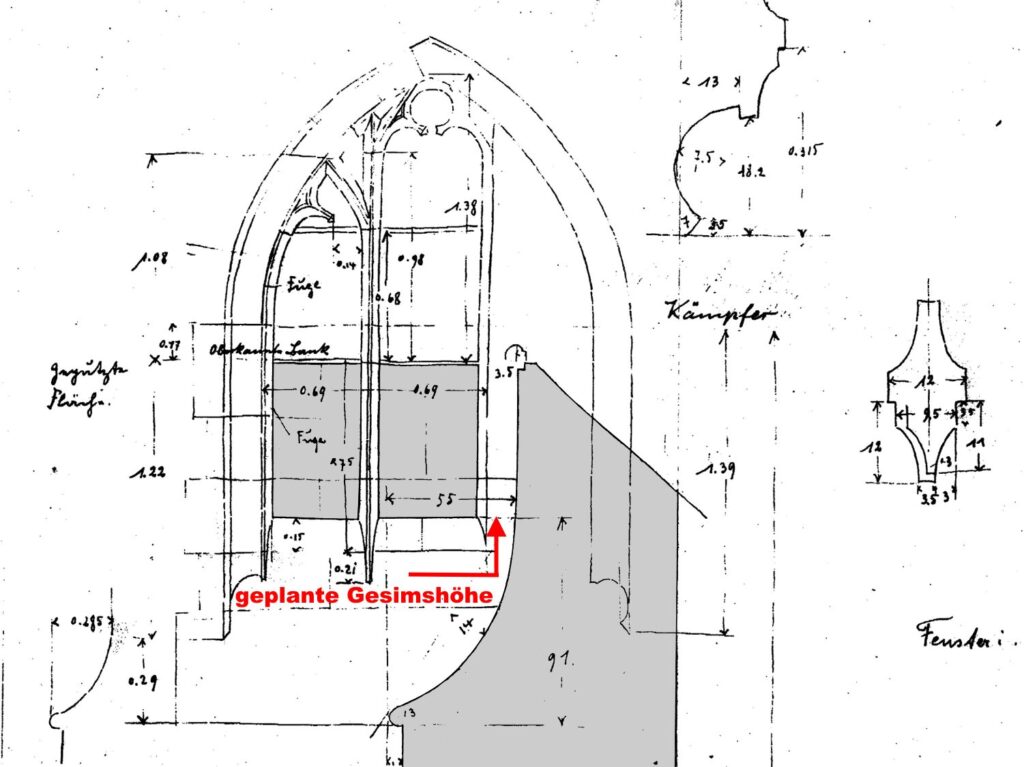
Die Höhenentwicklung von Mittel- und Seitenschiff im Aufriss:
Die Höhe, bis Oberkante Kapitell beträgt lt. Aufmaß 14,35m. Beide Seitenmaße der Grundfläche ergeben mit 8,358m + 5,91m zusammen eine Höhe von 14,268m, die Differenz zum Aufmaß = 8,2cm. Die Gewölbehöhe über dem Kapitell beträgt bis zum Gewölbescheitel 5,91m und entspricht damit 10 Ellen oder genau einer Jochlänge.
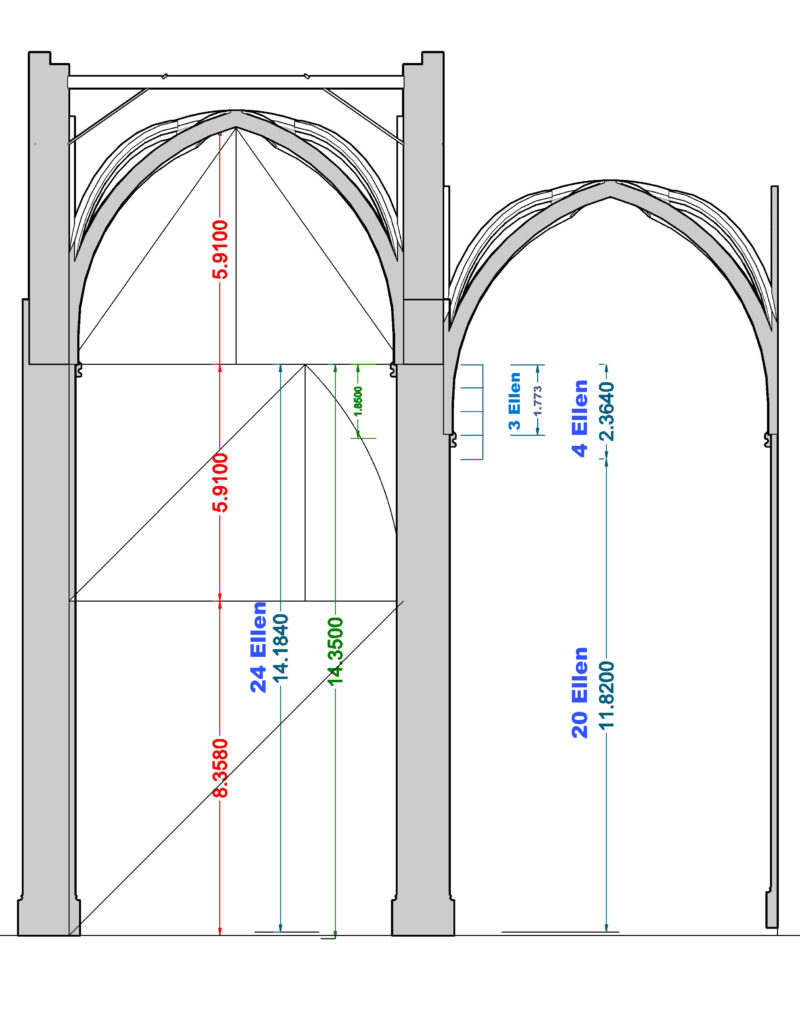
Die Kapitellhöhe in den Seitenschiffen lag lt. Aufmaß 1,85m niedriger als im Hauptschiff. Eine Höhenentwicklung nach der Methode „ad quadratum“ ist hier zunächst nicht so deutlich erkennbar wie im Mittelschiff
Nach einer erneuten Planänderung sollten die Seitenschiffe in gleicher Grundrissgröße aber mit niedrigeren Gewölbehöhen ausgeführt werden. Das Modell zeigt die geplante Änderung
Mich interessierte, ob auch diese geänderte Planung nach den Regeln „ad quadratum“ ausgeführt werden sollte.
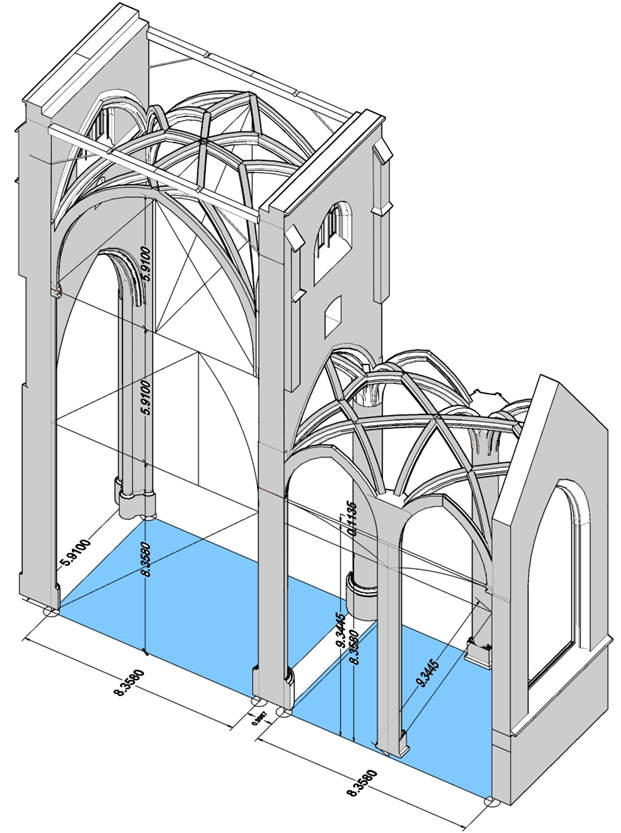
Die geometrische Konstruktionsmethode „ad quadratum“ ergibt im Seitenschiff eine Kämpferhöhe von 9,3445m, die CAD-Zeichnung eine Höhe von 9,458m. Die Differenz beträgt 11,35cm.
Die Kämpferhöhe von 9,458m entspricht aber fast exakt der Höhe von 16 Ellen à 0,591m = 9,456m. Die Vermutung liegt nahe, dass Höhenmaße auf der Baustelle in Elle und Fuß ermittelt wurden und nicht nach der Regel „ad quadratum“ bzw. 1: √2 .
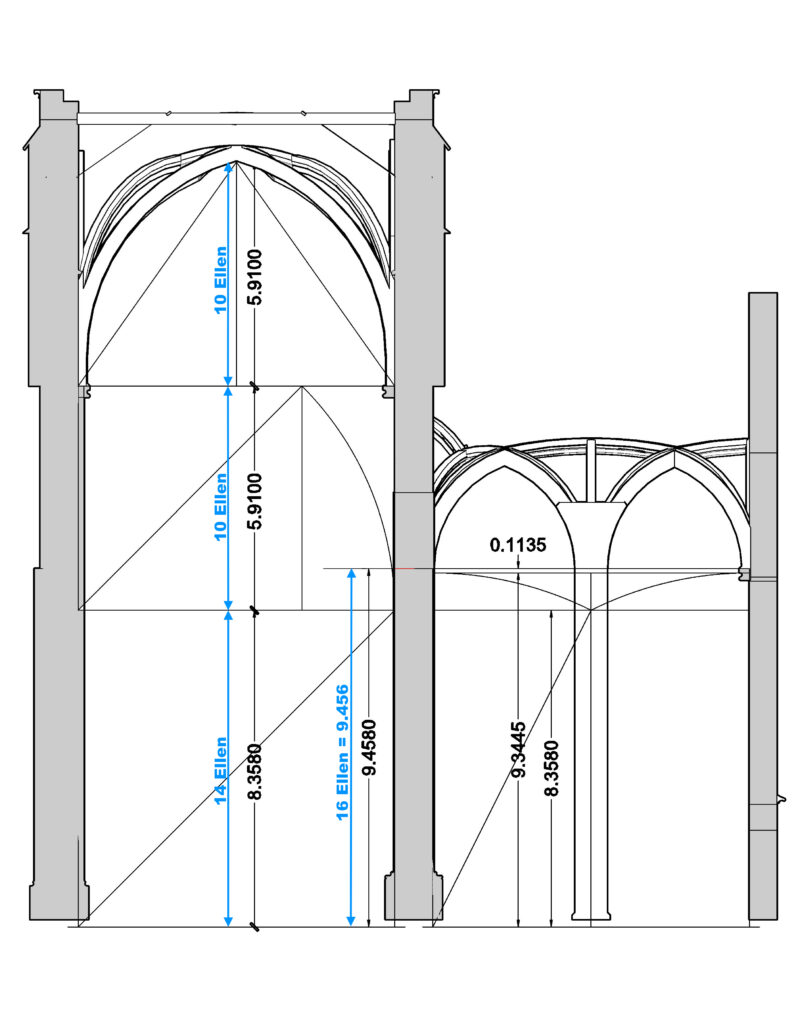
Die unterschiedlichen Maßdifferenzen waren der Anlass zu Überlegungen über die Anwendung und Praxistauglichkeit der Regel „ad quadratum“.
War die Konstruktionsmethode „ad quadratum“ auf einer Baustelle überhaupt sinnvoll?
Die Regel „ad quadratum“ ist auf einer ebenen Fläche wie einem Bauplatz oder einem Schnürboden, mit Zirkel, Schnur und Richtscheit sehr einfach anzuwenden. Aber zum Einmessen von Höhen auf einer Baustelle?
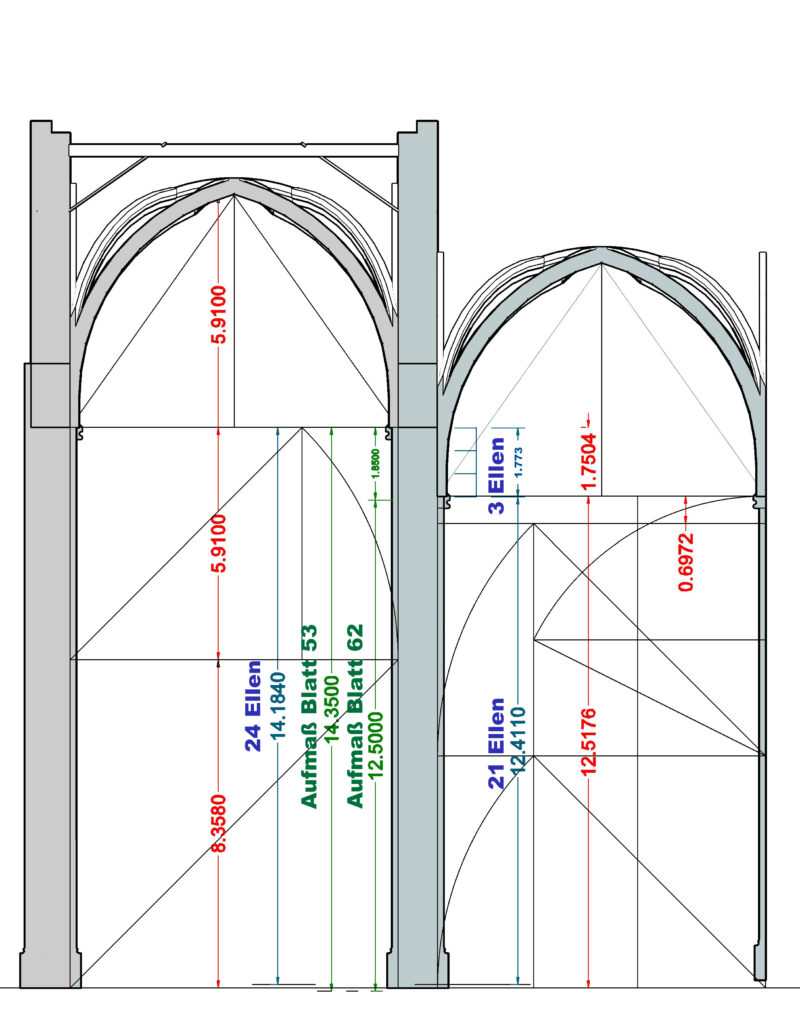
Ich habe deshalb in dieser Zeichnung unterschiedliche Mess-Methoden und -ergebnisse nebeneinander zum Vergleich eingetragen,
grün: Maße lt. Aufmaß Plan Nr. 53 und 62
rot: Maße gem. 1: √2 „ad quadratum“
blau/schwarz: Maße in Ellen
Vergleich 1:
Höhenunterschied zwischen den Gewölbeanfängern von Mittelschiff und Seitenschiff
lt. Aufmaß Blatt 53 und 62: 14,35m – 12,50m = 1,85 m
lt. Methode „ad quadratum“ (rotes Maß) = 1,7504 m
mit Knotenleine 3 Ellen (blaues Maß) = 1,773 m
Die geringe Maß-Differenz von ca. 7,7 cm zwischen dem Aufmaß und der Maßermittlung nach Ellen lässt vermuten, dass auf der Baustelle die Formel 1:1,41 nicht benutzt wurde.
Vergleich 2:
Höhenermittlung der Gewölbeanfänger des Seitenschiffs:
lt. Aufmaß Blatt 62 = 12,50m
lt. Methode „ad quadratum“ (rotes Maß) = 12,5176 m
mit Knotenleine 21 Ellen = 12,4110 m
hier ist das Einmessen nach „ad quadratum“ sehr kompliziert und die Maßdifferenz in Ellen mit 8,9 cm ebenfalls sehr gering
Ein Seitenverhältnis von 10 zu 14 weicht nur unwesentlich von dem Ideal-Verhältnis „ad quadratum“ bzw. 1: √2 oder 1:1,41 ab. Da es aber an einer Baustelle viel einfacher einzumessen ist, vermute ich, dass diese Annäherung an die Ideal-Regel beim Bau des Überlinger Münsters angewendet wurde.
Im Folgenden möchte ich die Regel „ad triangulum“ am Maßwerk einiger Fenster des Überlinger Münsters untersuchen
Maßwerk
Mit Maßwerk bezeichnet man in der Architektur die filigrane Arbeit von Steinmetzen zur Gliederung von Fenstern, Balustraden und geöffneten Wänden. Das Maßwerk besteht aus geometrischen Mustern, die als Steinprofile umgesetzt werden, wobei der Stein komplett durchbrochen wird.
Gewände
Als Gewände bezeichnet man die Laibung eines Portals oder Fensters, wenn sie schräg geführt ist. Das Gewände wird im Verlauf der Gotik zunehmend plastischer gestaltet und durch Stufungen, Profile und Säulchen gegliedert, bis die Flächigkeit der Mauer optisch ganz in plastische Formen aufgelöst scheint.
Wikipedia
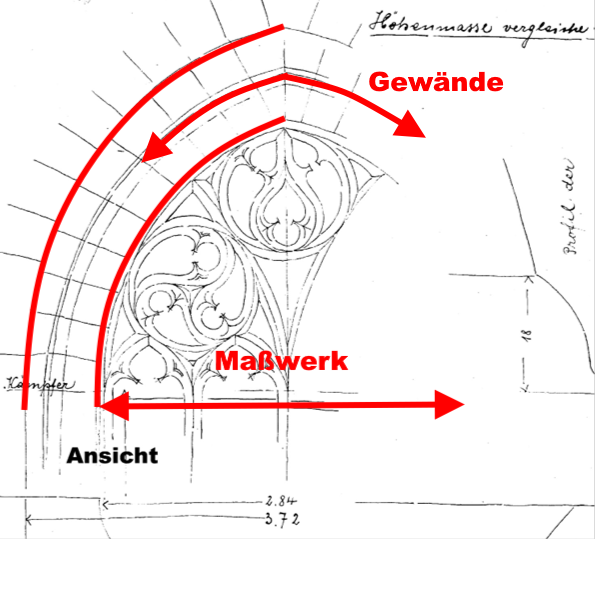
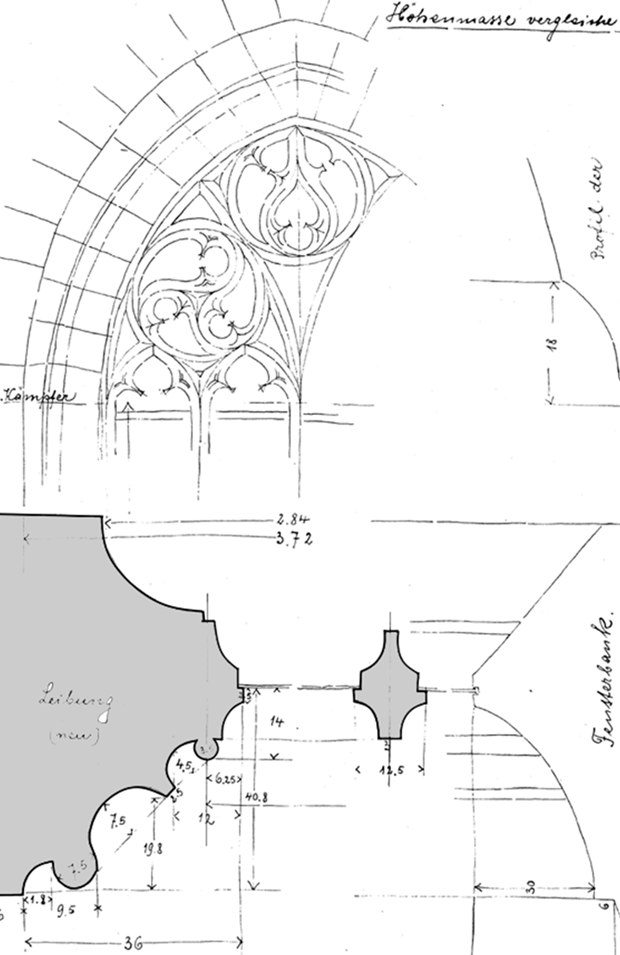
die folgende Zeichnung zeigt den Querschnitt des Gewände- und Maßwerkprofils am mittleren Chorfensters gem. Aufmaß Blatt 28
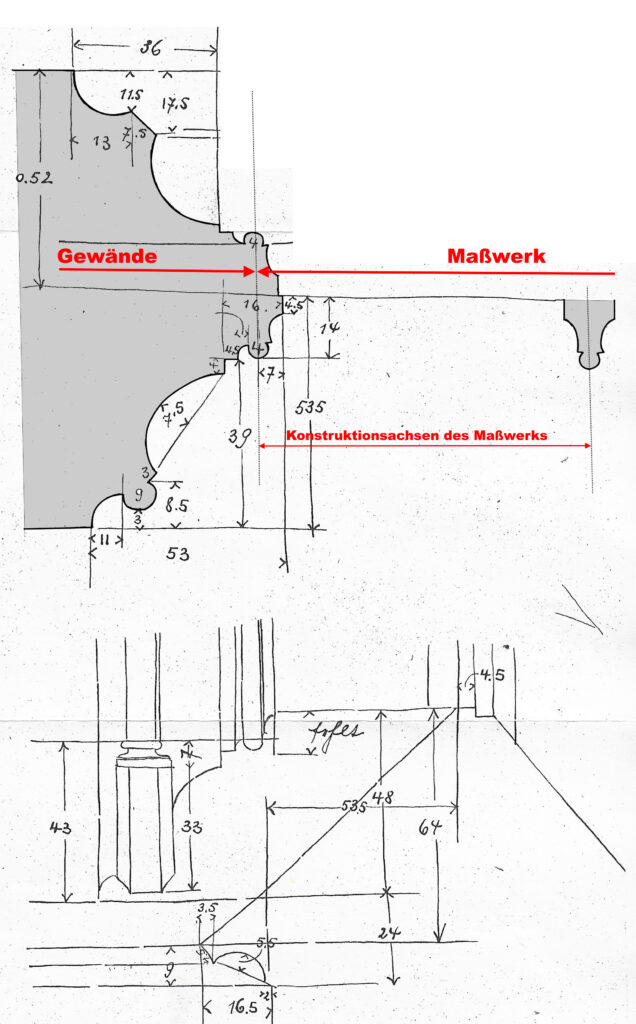
C. zunächst ein Vergleich einiger Grundformen gotischer Fenstermaßwerke „tringulum in quadratum“
1. schmale Form: gleich-schenkliges Dreieck im Quadrat
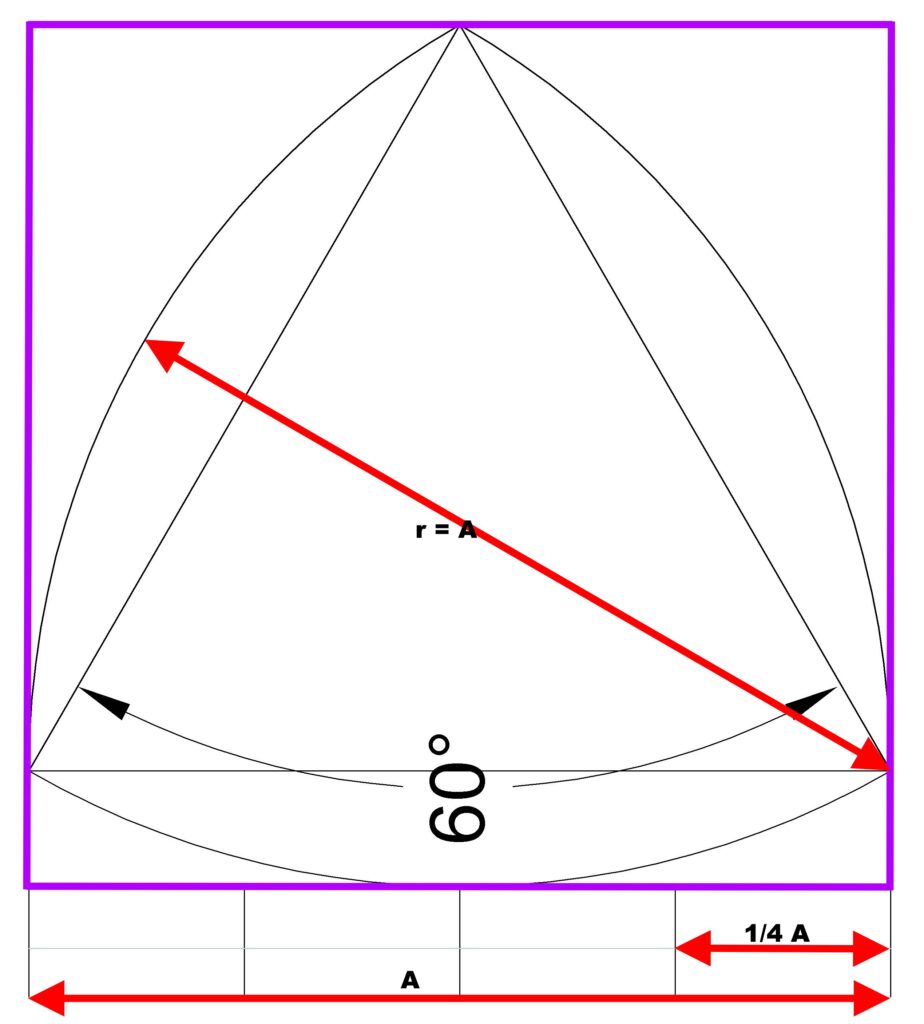
2. mittlere Form: gleich-seitiges Dreieck im Quadrat
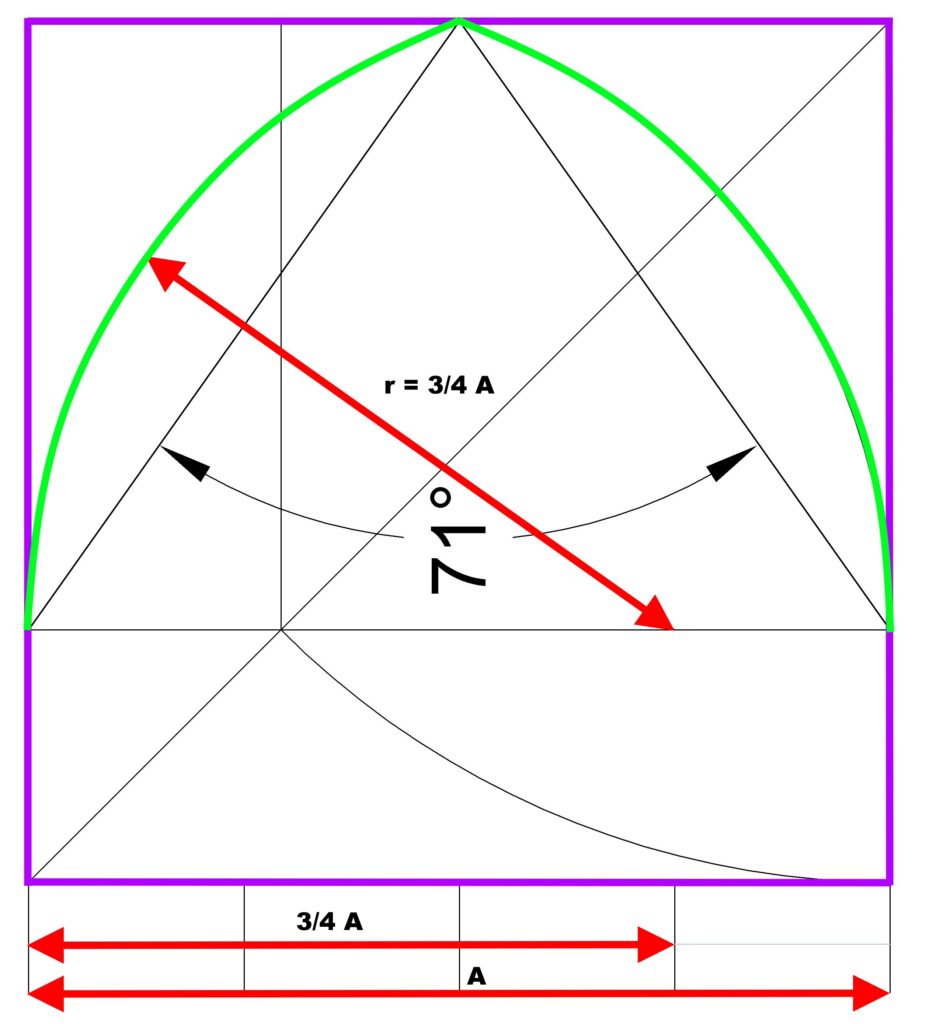
3. breite Form: gleich-schenkliges Dreieck in einem Rechteck, unterteilt nach der Regel „ad quadratum“
C1: das Maßwerk des mittleren Chorfensters

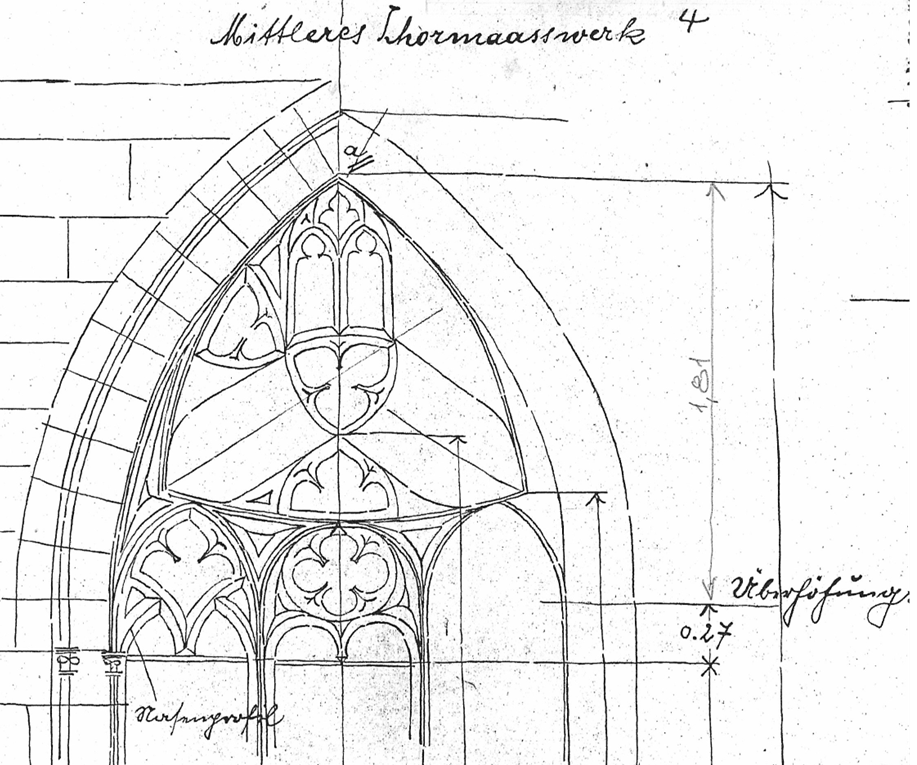
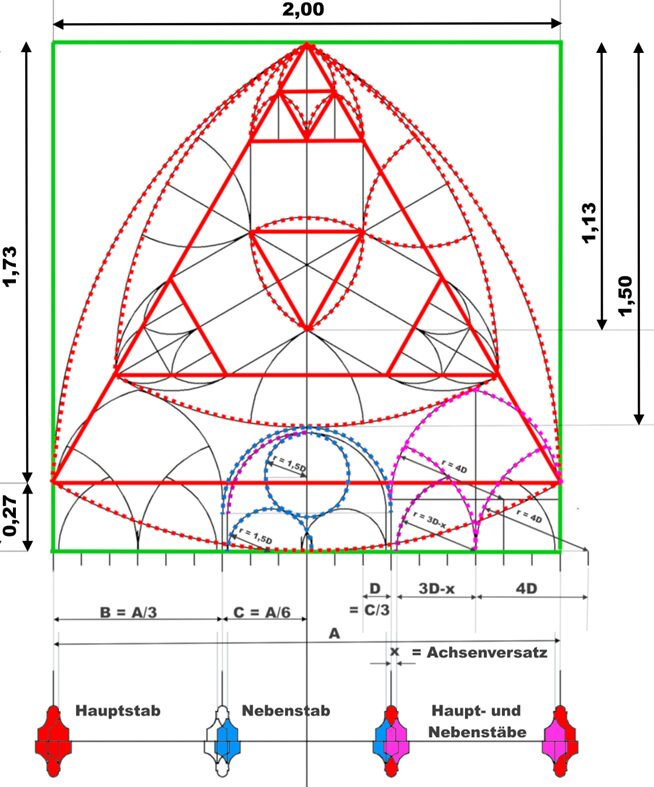
Aus der Aufmaß-Zeichnung Blatt Nr.28 ergibt sich, dass die äußeren Konstruktionslinien des gesamten Maßwerks (ohne Leibung) ein Quadrat bilden.
In dieses Quadrat ist eingeschlossen ein gleichseitiges Dreieck, über dessen Seitenlinien ein Bogen mit dem Radius der Seiten-länge des Quadrats den oberen Teil des gotischen Maßwerks über dem Kämpfer bildet
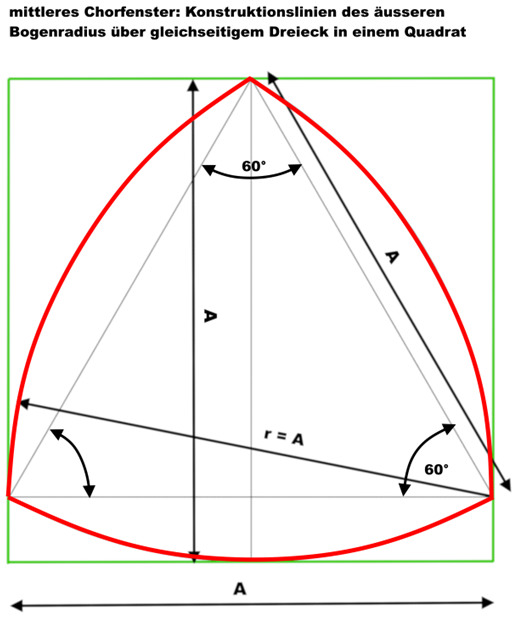
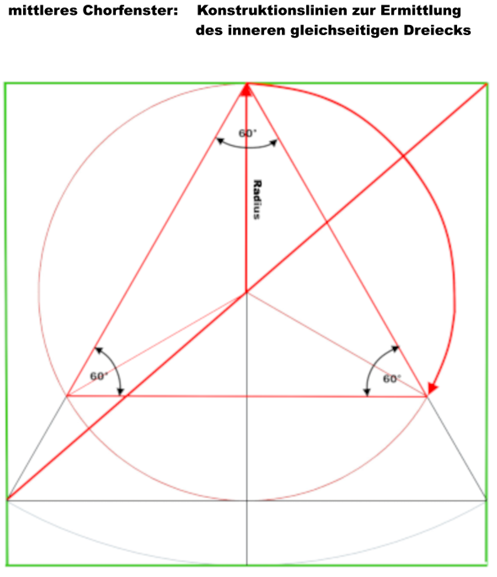
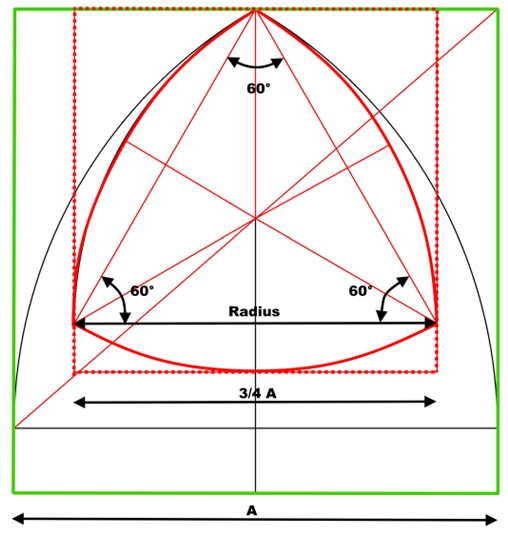
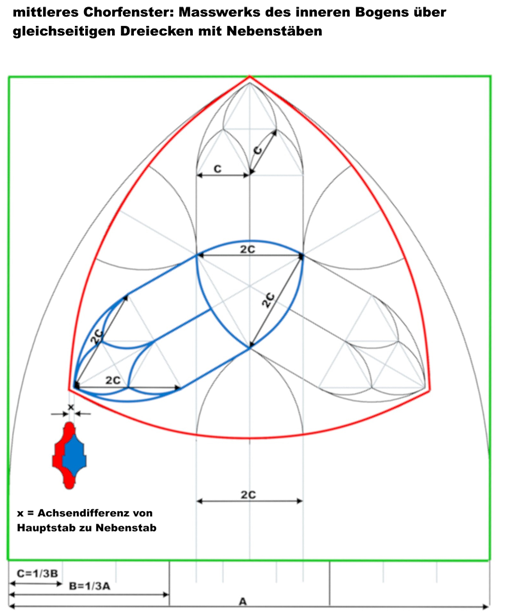
die einzelnen Konstruktionsschritte für das Maßwerk sind hier dargestellt:
der obere Teil des Maßwerks ist nur aus Kreissegmenten über gleichseitigen Dreiecken gebildet, der untere Teil aus Segmenten mit verschiedenen Radien, die sich aus Zwei- oder Dreiteilungen der Fensterbreite ergeben
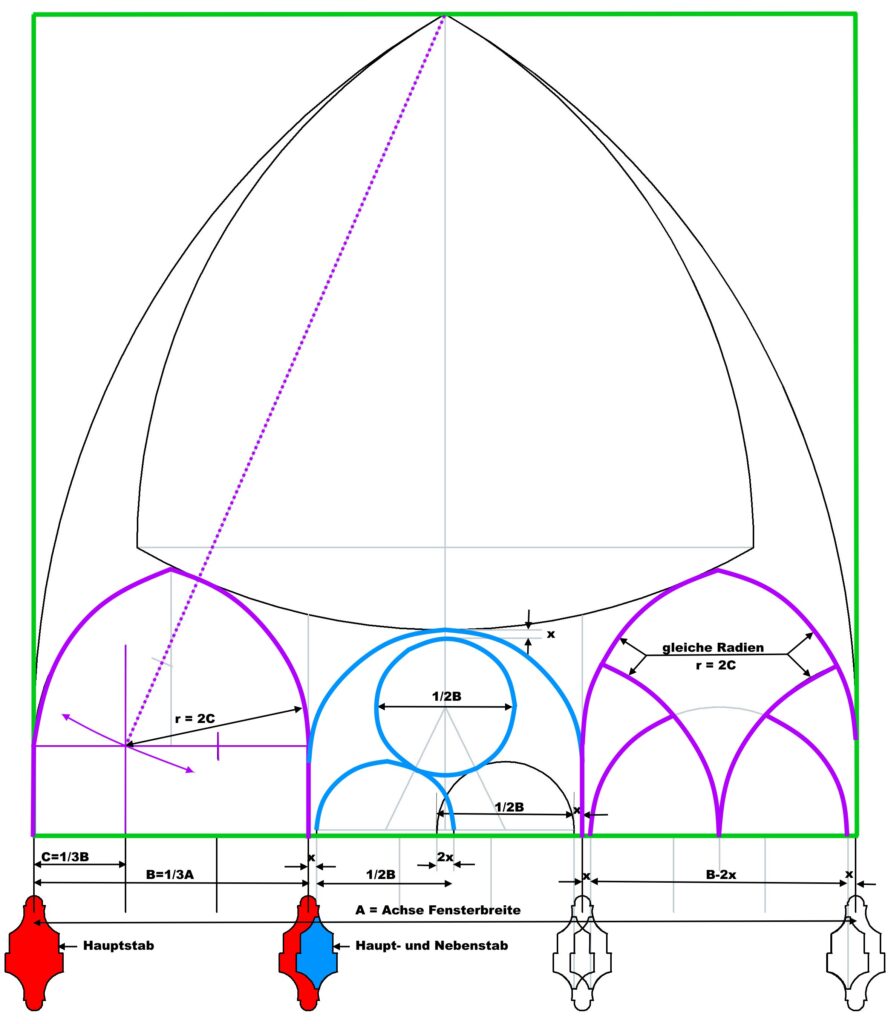

C2: das Maßwerk des mittleren Giebelfensters

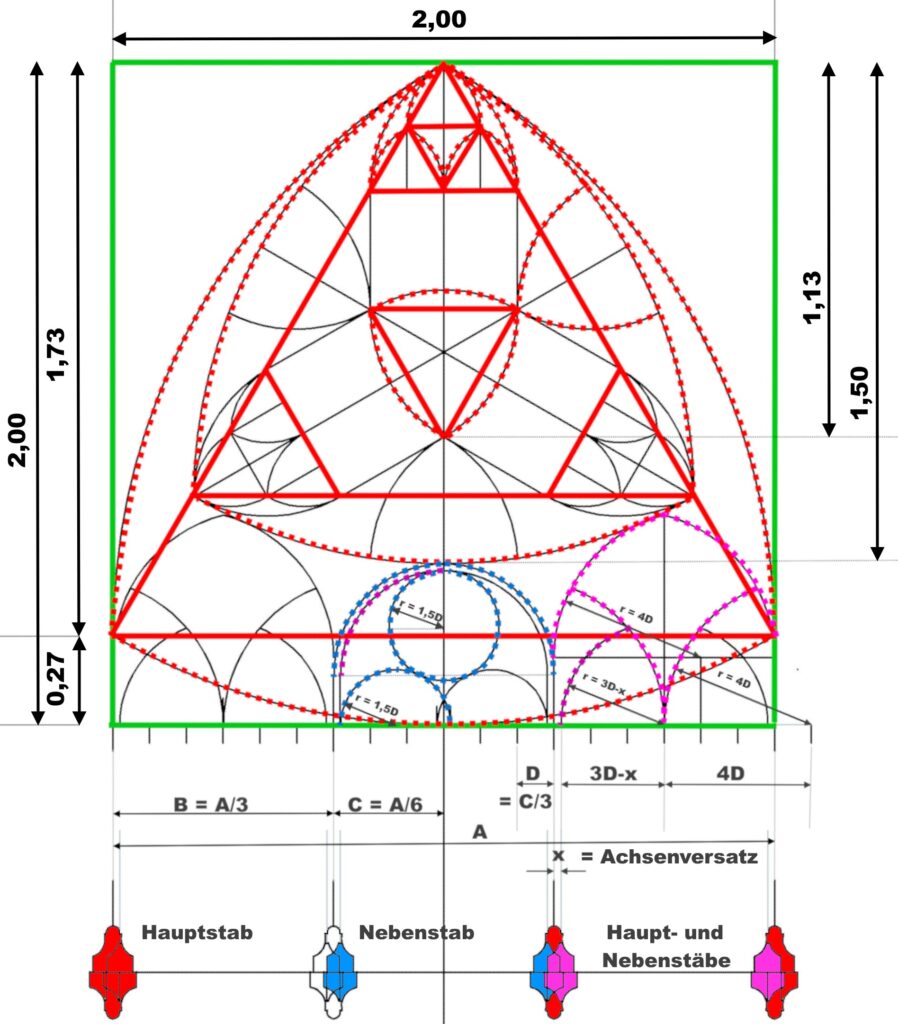
das Aufmaß Blatt Nr.49 führt zu folgender Konstruktionsweise
Das mittlere Giebelfenster hat eine breite Form und ist viergeteilt.
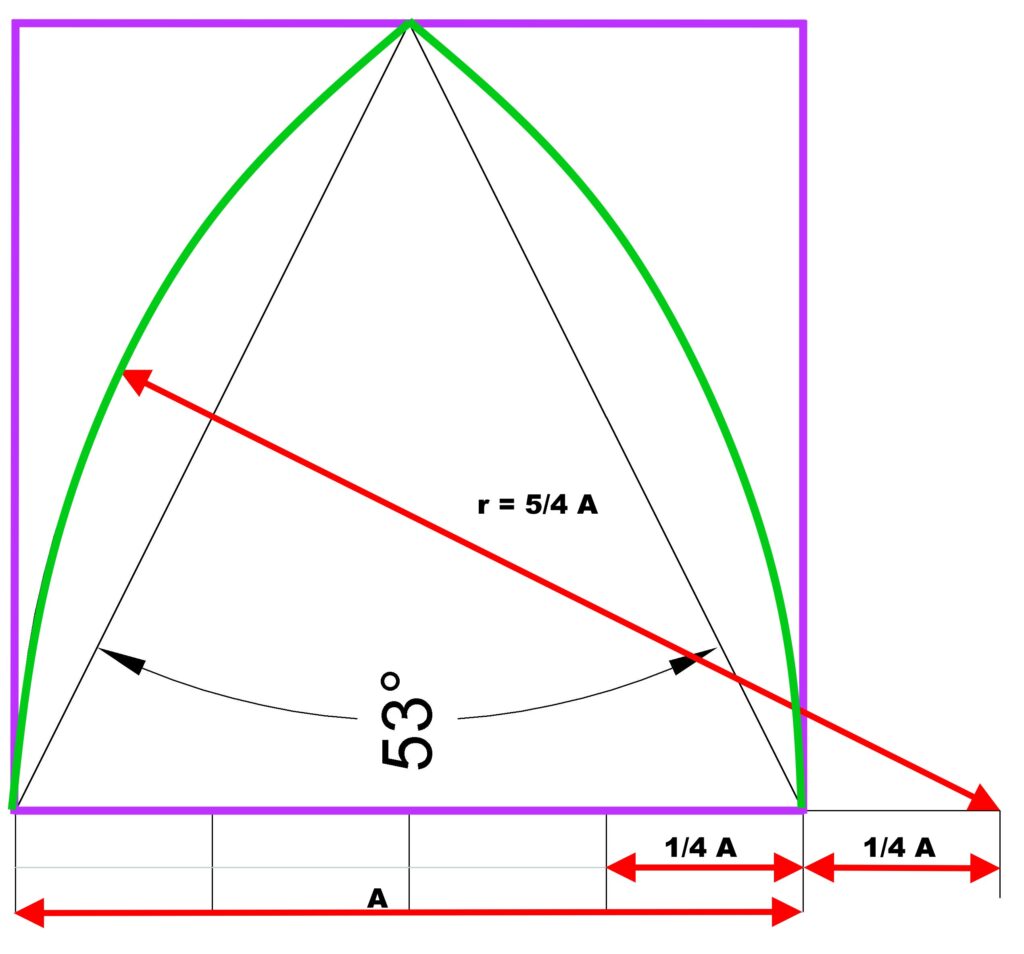
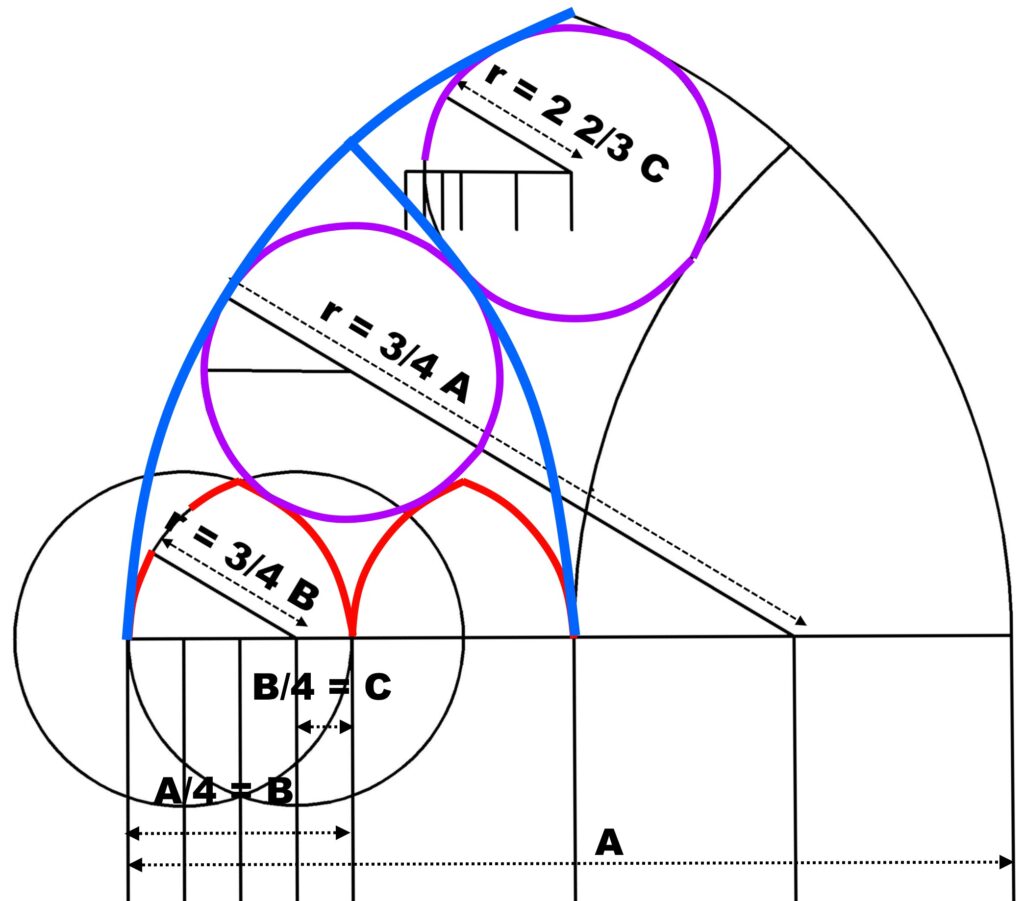
Dies Maßwerk ist nicht über einem Quadrat oder gleich-seitigen Dreieck entworfen, sondern über einem nach den Regeln des „ad quadratum“ gebildeten Rechteck. Der Radius der Kreisseg-mente beträgt 3/4 der Gesamt-Fensterbreite.
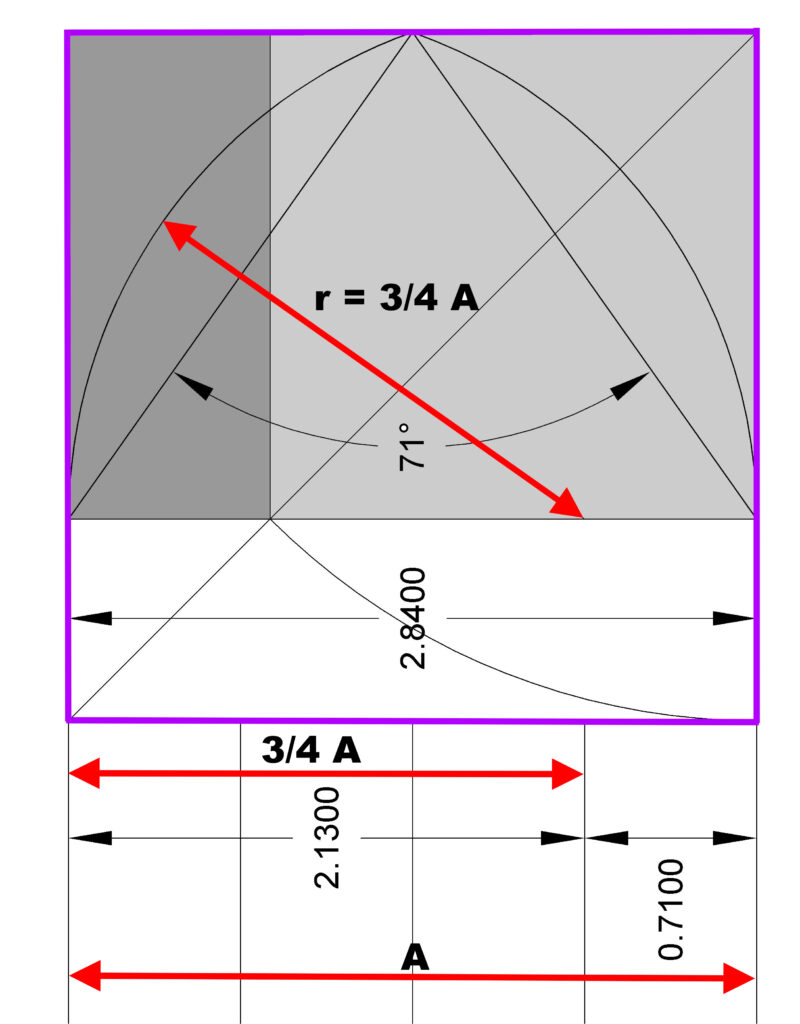
Je 2 Fensterfelder sind durch symmetrische Bogensegmente zusammengefasst, die in ihrer Spannung den äußeren Bögen des Maßwerks entsprechen. Jedes einzelne Fensterfeld ist nach dem gleichen Konstruktionsprinzip durch Bogensegmente mit r=3/4 Fensterbreite geschlossen. Die 3 oberen eingeschlossenen Kreise sind gleich groß. Ihr Radius beträgt zwei2/3 der Breite eines Fensterteiles C.
C3: das Maßwerk des Fensters im Obergaden

Die Fenster im Obergaden gem. Aufmassblatt 59
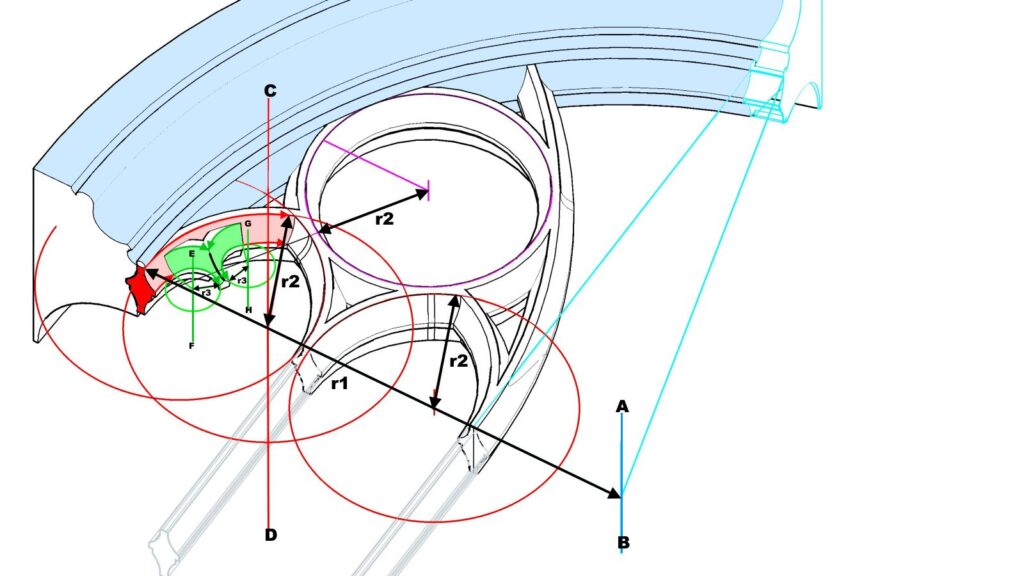
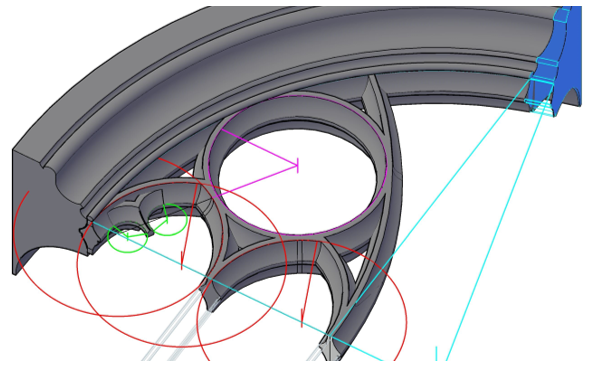
Die Konstruktion eines sehr breiten Maßwerks, eines „triangulum“ in „qudratum“
Die Gesamtbreite wird aufgeteilt in 3 Fensterbahnen und diese wiederum 4-fach geteilt. Jedes Einzelteil, hier mit C bezeichnet, beträgt also 1/12 der Gesamtbreite.
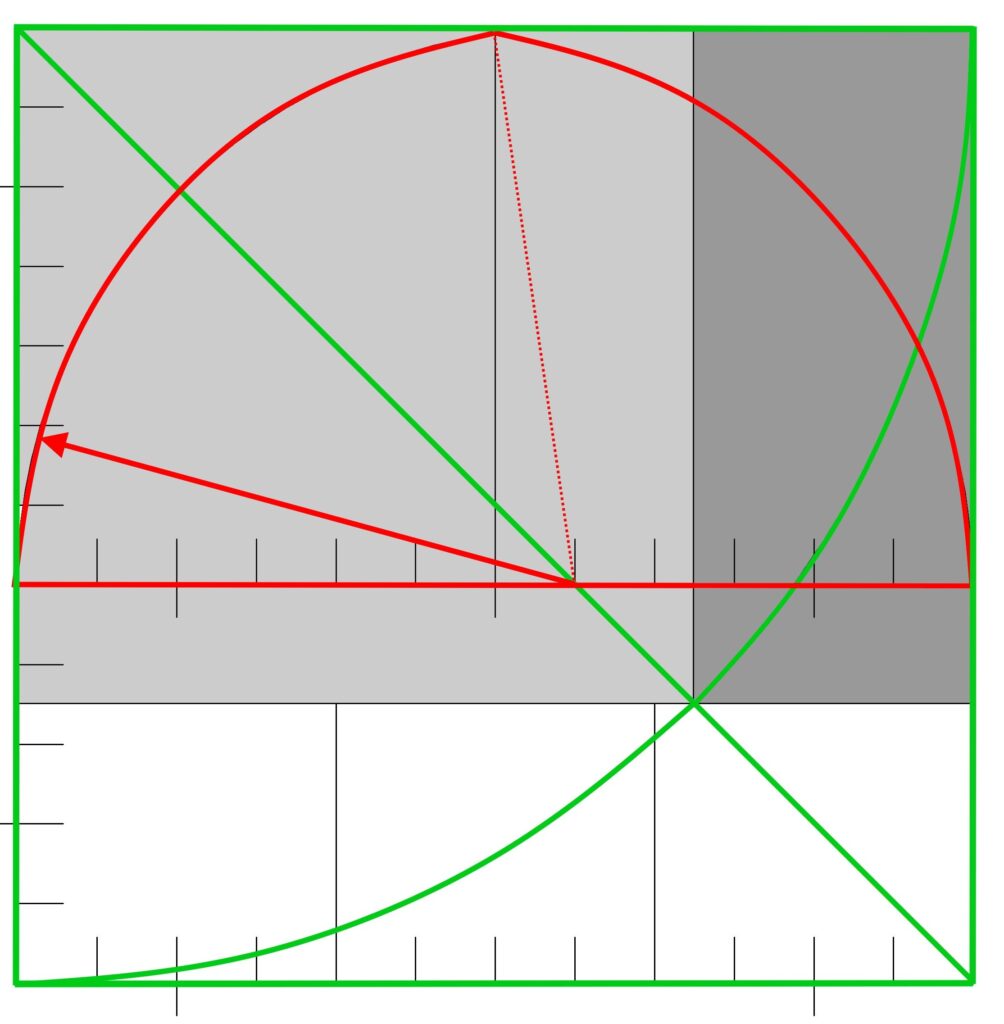
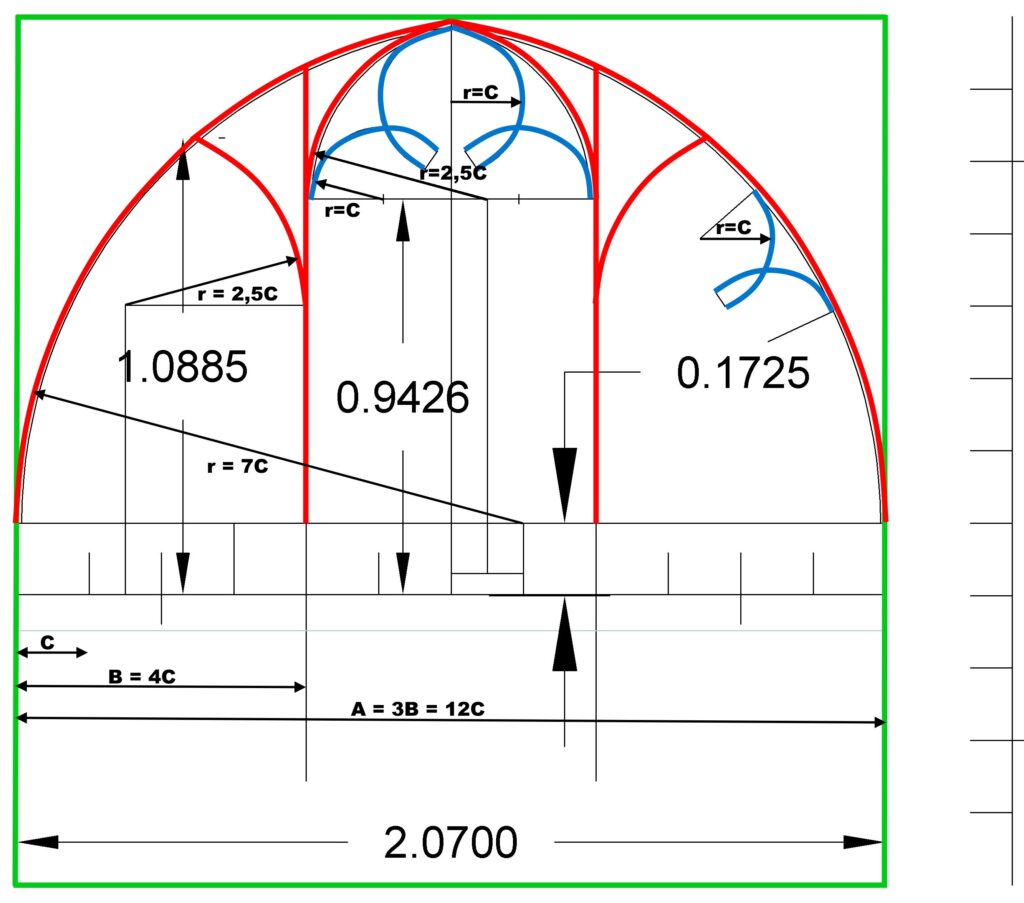
.
Das Maß C bildet das Grundmaß für die Bogenradien im Fenstermaßwerk: der Radius des großen äußeren Bogens beträgt 7 x C, die kleineren Bögen 2,5 x C und für die „Nasen“ beträgt der Radius 1 x C. Die „Nasen“ ergeben sich durch die Überschneidung der Radien bzw. der Profile.
Das Ergebnis dieser Untersuchungen
In der ersten gotischen Bauphase ab 1350 wurden für den neuen Chorraum die durch die romanische Basilika vorgegebenen Raummaße übernommen: die alten Wände des romanischen Rechteckchores ergaben die neue Breite des neuen gotischen Chores mit 5/8 Abschluss und die flache Decke des romanischen Kirchenschiffs war bestimmend für die Höhe des Triumphbogens und der anschließenden einfachen Kreuzgewölbe im Chorraum.
Die Regel des „ad quadratum“ wurde ganz sicher aber bei Entwurf und Konstruktion des zweiten gotischen Bauabschnitts ab 1420 angewendet. Auf ihr basiert der Entwurf der großen geplanten Hallenkirche und nach einer Planänderung auch der Entwurf der niedrigeren Seitenschiffe.
Die Anwendung dieser Regel ist die Ursache dafür, dass das Mittelschiff schmaler wurde als der Chorraum und ebenso für gestalterische Anschlussprobleme zwischen Chor und Mittelschiff.
Auch ist hier der Grund dafür zu sehen, dass der Bauplatz für die Planung offensichtlich zu klein wurde und die Nordwestecke des Giebels auf das vorhandene Ziegelmauerwerk des Pfarrhauses aufgesetzt werden musste und an der Südwestecke wegen des Verlaufs der Grundstücksgrenze zum Haus der Beginen der Giebel abgeschrägt wurde.
Nach Aufgabe dieser Planungsphasen 1429 und nach dem Weiterbau zu einer fünfschiffigen Basilika ist die Anwendung der Regel „ad quadratum“ mit Ausnahme im Mittelschiff, das nach der alten Planung ausgeführt wurde, in den Seitenschiffen für mich nicht mehr erkennbar. Auch die Fertigstellung der Fenstermaßwerke war nach den Regeln „ad triangulum“ nicht mehr möglich. Sie erhielten notgedrungen einen Tudorbogen-Abschluss.
Carl Fahr, Überlingen, 2024
Schreibe einen Kommentar